
Chu Vi Hình Tam Giác- Bài Tập Củng Cố Dễ Hiểu
Chu vi tam giác là một kiến thức cơ bản được tìm hiểu trong chương trình tiểu học. Việc nắm rõ công thức này giúp ta áp dụng kiến thức trong tính toán và thực tế. Cùng chúng tôi tìm hiểu rõ hơn về nội dung này trong bài viết dưới đây nhé!
Công thức tính chu vi hình tam giác
Chu vi hình tam giác có công thức cơ bản: P = a + b + c
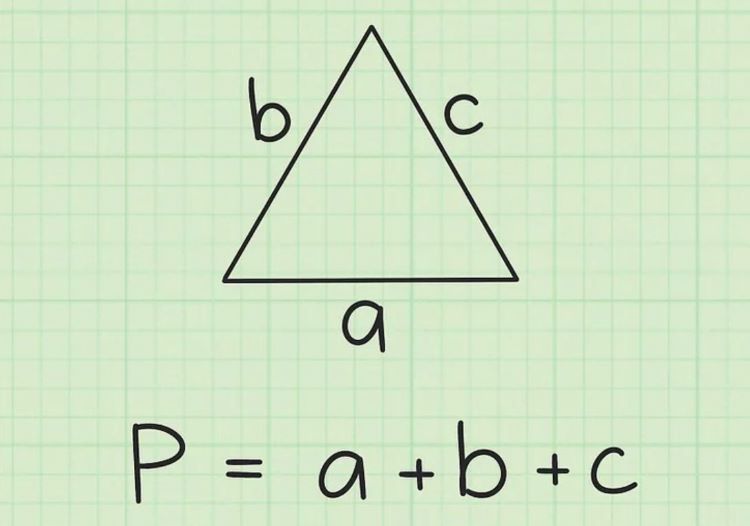
Trong đó a, b, c lần lượt là độ dài 3 cạnh của tam giác. Để tính chu vi tam giác ta tính tổng độ dài các cạnh lại với nhau.
Ví dụ: Cho tam giác có độ dài 3 cạnh là a = 8 cm, b = 9 cm và c = 12 cm.
Ta có thể tính chu vi hình tam giác như sau:
P = a + b + c = 8 + 9 + 12 = 29 cm.
Đây là công thức cơ bản để tính chu vi của tam giác. Nó áp dụng cho tất cả các loại tam giác, không chỉ tam giác bình thường mà còn tam giác cân hay tam giác đều.
Mở rộng tính chu vi hình tam giác theo cách khác?
Với tam giác không đều, chúng ta không thể sử dụng công thức chu vi tam giác đơn giản P = a + b + c để tính chu vi tam giác. Khi đó, chúng ta phải biết độ dài của từng cạnh của tam giác không đều để tính toán.
Trong trường hợp biết hệ tọa độ của các đỉnh tam giác. Ta có thể sử dụng công thức khoảng cách Euclid để tính độ dài 3 cạnh tam giác:
P = √(x1^2+ y1^2)+√(x2^2+ y2^2)+ √(x3^2+ y3^2)
Trong đó,
(x1, y1) và (x2, y2), (x3, y3) là tọa độ của các đỉnh tam giác.
>> Tham khảo: Công thức cấp số nhân
Các tính chất về chu vi tam giác mà chúng ta cần biết?
Ngoài cách tính chu vi tam giác thông thường kể trên, có một số tính chất chu vi mà bạn cần lưu ý:
- Tính chất cơ bản: Chu vi tam giác sẽ tổng độ dài của ba cạnh tam giác và được kí hiệu là P. Công thức tính chu vi tam giác có dạng P = a + b + c. Trong đó a, b, c lần lượt là độ dài 3 cạnh tam giác.
- Tính chất Bất đẳng thức trong tam giác: Tổng độ dài hai cạnh của tam giác luôn lớn hơn độ dài 1 cạnh còn lại. Điều này được thể hiện bằng ba biểu thức: a + b > c, b + c > a, a + c > b. Nếu như một trong ba biểu thức này không đúng thì tam giác đó không hề tồn tại. Ngược lại độ dài 1 cạnh của tam giác luôn lớn hơn hiệu độ dài 2 cạnh của tam giác. Tức là a-b< c, b-c < a, hay a- c < b.
- Cách tính chu vi tam giác đều: Trong tam giác đều, ba cạnh tam giác đều sẽ có độ dài bằng nhau. Vì vậy, để tính chu vi tam giác đều, ta có thể nhân độ dài một cạnh với hệ số 3: P = 3a.
- Tính chất chu vi của tam giác vuông: Trong tam giác vuông, chu vi tam giác sẽ bằng tổng độ dài hai cạnh góc vuông cộng với với độ dài cạnh còn lại. Ví dụ, nếu cạnh góc vuông là a và b, và cạnh còn lại là c, thì ta có chu vi tam giác là P = a + b + c.
- Tính chất chu vi của tam giác cân: Trong tam giác cân, hai cạnh tam giác bên sẽ có độ dài bằng nhau. Vì vậy, để tính chu vi tam giác cân, ta có thể nhân độ dài một cạnh bên với số 2 và cộng với độ dài cạnh đáy. Tức: P = 2a + b.
- Tính chất chu vi tam giác đều giản định: Trong một tam giác đều, chu vi tam giác sẽ bằng tích độ dài một cạnh và số 3: P = 3a.
- Tính chất chu vi tam giác tù: Trong tam giác tù thì chu vi tam giác bằng tổng độ dài ba cạnh tam giác. Tức: P = a + b + c.
Những tính chất trên là những kiến thức cơ bản về cách tính chu vi tam giác mà chúng ta cần biết để tính và hiểu về tam giác.
>> Xem thêm: Mệnh kim hợp hướng nào
Công thức tính diện tích tam giác
Ngoài cách tính chu vi tam giác, công thức tính diện tích tam giác được áp dụng khá phổ biến:
Công thức tổng quát
S= ½ a x h
Trong đó: a là độ dài cạnh đáy của tam giác, h là chiều cao ứng với cạnh đáy tương ứng.
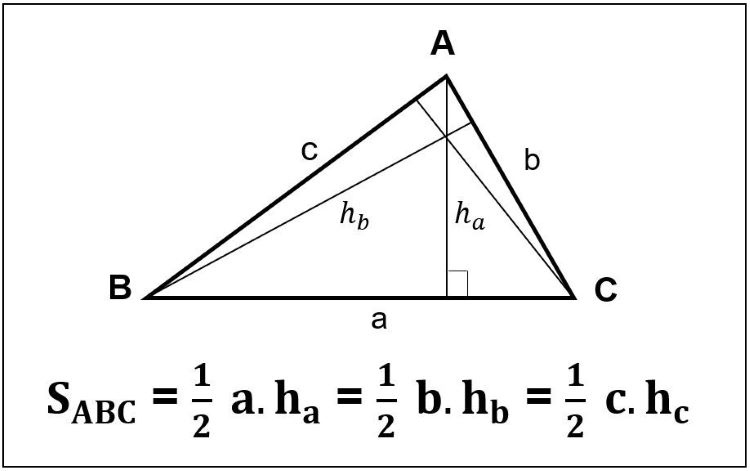
Đối với tam giác thường
S= ½ a x h
Đối với tam giác cân
S= ½ a x h
Đối với tam giác đều
S= ½ a x h
- Đối với tam giác vuông:
S= ½ a x b (a, b là độ dài 2 cạnh góc vuông)
- Đối với tam giác vuông cân:
S= ½ a^2 (a là độ dài cạnh góc vuông)
Tham khảo: Nước ion kiềm mua ở đâu?
Bài tập củng cố kiến thức tính chu vi tam giác có đáp án
Bài 1: Cho tam giác ABC có 3 cạnh lần lượt là 4 cm, 5 cm và 8 cm. Tính chu vi hình tam giác này là bao nhiêu:
Trả lời:
Chu vi hình tam giác ABC là P= a + b + c= 4+ 5 + 8= 17 (cm_
Vậy chu vi của hình tam giác đã cho là 15cm
Bài 2: Tìm độ dài của cạnh c của tam giác nếu P = 30cm và a = 8 và b = 10 cm
Trả lời:
Áp dụng công thức tính chu vi P = a + b + c,.
Thay vào công thức trên P=30, a=8 và b = 10 ta có:
30 = 8+ 10+ c
30 = 18 + c => c= 12cm
Bài 3: Độ dài cạnh một cạnh của tam giác cân sau đây bằng bao nhiêu cm. Khi biết độ dài cạnh không bằng nhau là 5cm và chu vi tam giác là 17cm.
Trả lời:
Vì đề bài cho tam giác cân nên độ dài 2 cạnh bên bằng nhau. Đặt là a
Ta có chu vi tam giác đã cho là P = a + a + 5
=> 17 = 2a + 5 => 2a = 12
⇔ a = 6cm
Như vậy độ dài 2 cạnh bằng nhau của tam giác cân là 6cm.
Bài 4: Một tam giác vuông ABC có độ dài 2 cạnh bên lần lượt là 3cm và 4 cm. Tình chu vi của hình tam giác đó.
Ta có: AB = 3cm, AC = 4cm nên BC là cạnh huyền của tam giác.
Áp dụng định lý pytago:
=> BC^2= AB^2 + AC^2= 3^2+4^2= 25=> BC= 5
Chu vi tam giác đã cho là P= 3+4+5= 12 cm
Trên đây là những thông tin tổng quan liên quan đến chu vi tam giác. Hy vọng thông tin trên giúp ích cho bạn đọc. Đừng quên theo dõi những thông tin thú vị của Hoanggianoithat.vn nhé!
>> Xem thêm: Thi công tủ bếp tân cổ điển
Link nội dung: https://ausp.edu.vn/chu-vi-hinh-tam-giac-bai-tap-cung-co-de-hieu-a24319.html