21/12/2024 14:00

In bài này (Ctrl+P)

Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Chi Tiết Và Bài Tập

1. Khối chóp tứ giác đều là gì?

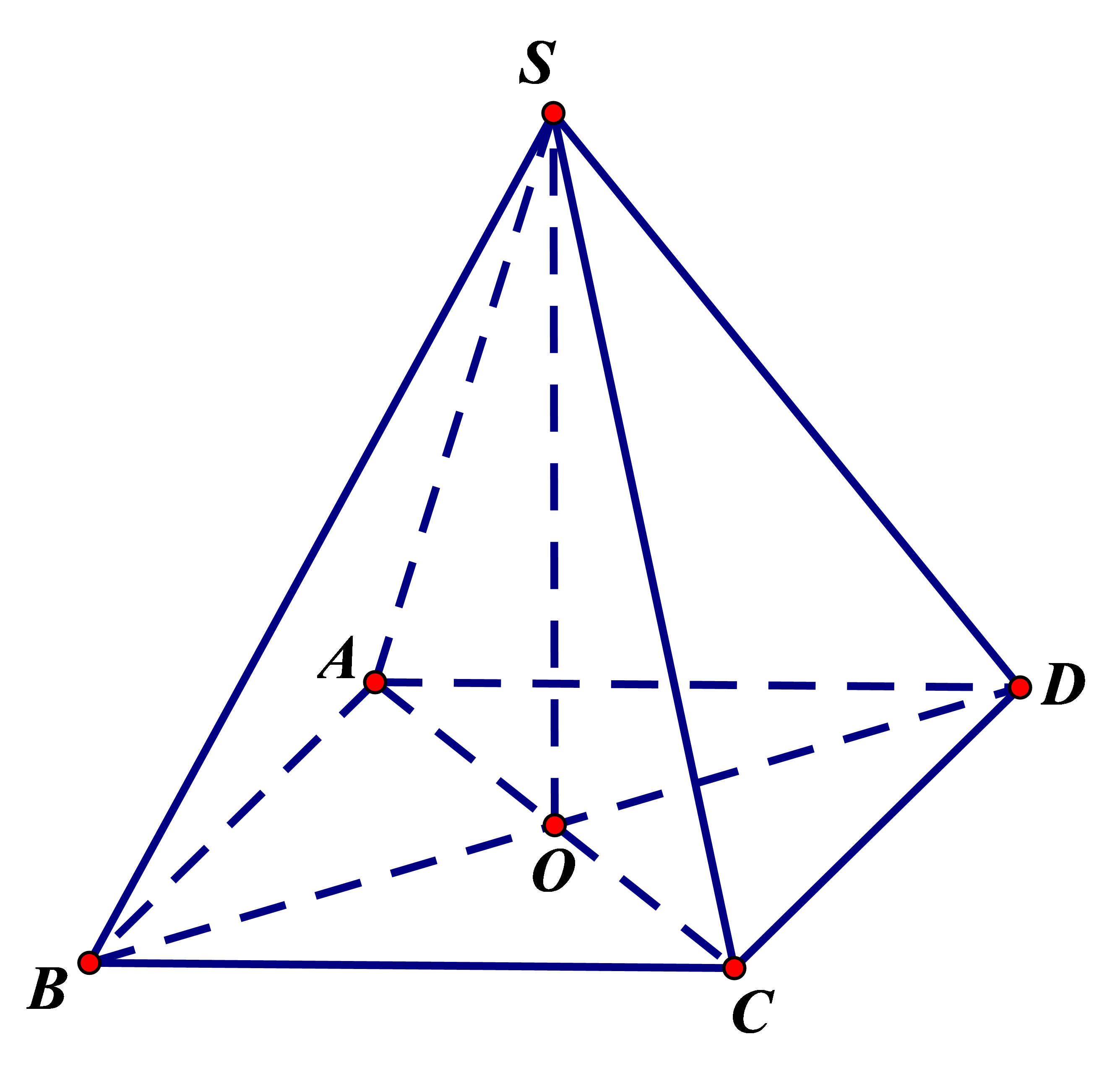
Là hình chóp có đáy là hình vuông, đường cao của chóp đi qua tâm đáy (giao của 2 đường chéo hình vuông).

2. Tính chất khối chóp tứ giác đều

- Cạnh bên bằng nhau

- Đáy là hình vuông

- Chân đường cao trùng với tâm mặt đáy

- Các mặt bên là các tam giác cân bằng nhau

- Các góc tạo bởi cạnh bên và mặt đáy bằng nhau

- Các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau

Ví dụ:

Với hình chóp tứ giác đều SABCD, ta có:

Tứ giác ABCD là hình vuông tâm O
SO $\perp$ (ABCD)
(ABCD)
SA=SB=SC=SD
(SA; (ABCD))=(SD;(ABCD))= (SB;(ABCD))=(SC;(ABCD))

Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Chi Tiết Và Bài Tập

3. Công thức tính thể tích khối chóp tứ giác đều

Công thức V = (1/3).Sđáy.h

Trong đó:

+ V: Thể tích hình chóp tứ giác đều.

+ h: Chiều cao hình chóp tứ giác đều.

+ Sđáy: Diện tích đáy hình chóp tứ giác đều.

4. Công thức tính diện tích khối chóp tứ giác đều

4.1. Tính diện tích xung quanh

Công thức: Sxq= 4.S

Trong đó:

+ Sxq: Diện tích xung quanh của hình chóp tứ giác đều.

+ S: Diện tích mặt bên của hình chóp tứ giác đều.

4.2. Tính diện tích toàn phần

Công thức: Stp = Sxq + Sđáy

Trong đó:

+ Stp: Diện tích toàn phần của hình chóp tứ giác đều.

+ Sxq: Diện tích xung quanh của hình chóp tứ giác đều.

+ Sđáy: Diện tích đáy của hình chóp tứ giác đều.

Trọn bộ bí kíp giải quyết mọi dạng bài tập hình học không gian

5. Một số bài tập tính thể tích khối chóp tứ giác đều (kèm lời giải chi tiết)

Câu 1: Cho S.ABCD là hình chóp đều. Tính thể tích khối chóp S.ABCD biết AB = a; SA = a. AB = a; SA = a.

Giải

$\Rightarrow SH = \sqrt{SA^{2} - AH^{2}} = \frac{a\sqrt{2}}{2}$

Diện tích của đáy ABCD: SABCD = a2

$\Rightarrow V_{S.ABCD} = \frac{1}{3}S_{ABCD}.SH = \frac{1}{3}a^{2}.\frac{a\sqrt{2}}{2} = \frac{a^{3\sqrt{2}}}{6}$

Câu 2: Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a.?

Giải

Ta có: Diện tích đáy ABCD là a2

$SO^{2} = SB^{2} - OB^{2} = a^{2} - (\frac{a\sqrt{2}}{2})^{2} = \frac{a^{2}}{2}$

Suy ra ta có: $SO = \frac{a\sqrt{2}}{2}$

Vậy thể tích khối chóp cần tìm là:

$V_{S.ABCD} = \frac{1}{3}.\frac{a\sqrt{2}}{2}.a^{2} = \frac{a^{3}\sqrt{2}}{6}$

Câu 3: Cho hình chóp tứ giác đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích khối chóp.

Giải

Thể tích khối chóp được tính theo công thức:

$V = \frac{1}{3}B.h$ với B = x2

Gọi điểm O là tâm của hình vuông và điểm I là trung điểm của đoạn thẳng CD

$\Rightarrow SI \perp CD$

Gọi chiều dài của đoạn SO là h

$\Rightarrow SI = \sqrt{SO^{2} + OI^{2}} = \sqrt{h^{2} + \frac{x^{2}}{4}}$

Có Sxq = 2SI.CD; Sxq = 2B

$2x\sqrt{h^{2} + \frac{x^{2}}{4}} = 2x^{2} \Rightarrow \sqrt{h^{2} + \frac{x^{2}}{4}} = x$

Từ đó suy ra:

$\Rightarrow h^{2} + \frac{x^{2}}{4} = x^{2} \Rightarrow \frac{3x^{2}}{4} = h^{2} \Rightarrow h = \frac{x\sqrt{3}}{2}$

Lúc đó ta có thể tích của hình chóp là:

$V = \frac{1}{3}x^{2}.\frac{x\sqrt{3}}{2} = \frac{x^{3}\sqrt{3}}{6}$

Câu 4: Cho hình chóp đều S.ABCD có cạnh bằng a và cạnh bên tạo với đáy góc 60 độ. Tính thể tích hình chóp đều S.ABCD.

Giải

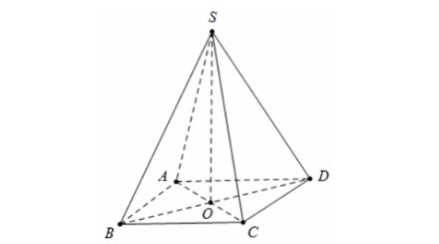
Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Chi Tiết Và Bài Tập

Gọi O là giao điểm của AC và BD $\Rightarrow SO \perp (ABCD)$

$\Rightarrow \widehat{SCO} = 60^{0} \Rightarrow tan60^{0} = \frac{SO}{OC} \Rightarrow SO = OC\sqrt{3} = \frac{a}{\sqrt{2}}.\sqrt{3}$

$\Rightarrow V = \frac{1}{3}a\sqrt{\tfrac{3}{2}}.a^{2} = \frac{a^{3}\sqrt{6}}{6}$

Câu 5: Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp 2 lần cạnh đáy. Tính thể tích khối chóp tứ giác đã cho.

Giải

Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Chi Tiết Và Bài Tập

Ta có $AC = a\sqrt{2} \Rightarrow AO = \frac{a\sqrt{2}}{2} \Rightarrow SO = \sqrt{SA^{2} - OA^{2}} = \frac{a\sqrt{14}}{2}$

Vậy $V_{S.ABCD} = \frac{1}{3}SO.S_{ABCD} = \frac{1}{3}.\frac{\sqrt{14}}{2}.a^{3} = \frac{\sqrt{14}}{6}a^{3}$

Câu 6: Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng $a\sqrt{3}$ . Tính thể tích của hình chóp đó theo a.

Giải

Gọi h là chiều cao của hình chóp đã cho, ta có:

$h = \sqrt{3a^{2} - \frac{a^{2}}{2}} = \frac{a\sqrt{10}}{2}$

$V = \frac{1}{3}S_{ABCD}.h = \frac{1}{3}a^{2}.\frac{a\sqrt{10}}{2} = \frac{a^{3}\sqrt{10}}{6}$

Câu 7: Chó hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng a. Tính thể tích khối chóp đó.

Giải

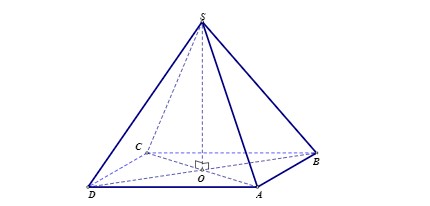
Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Chi Tiết Và Bài Tập

Xét hình chóp tứ giác đều S.ABCD

Ta có: $OD = \frac{a\sqrt{2}}{2}, SO = \sqrt{SD^{2} - OD^{2}} = \sqrt{2a^{2} - \frac{a^{2}}{2}} = \frac{a\sqrt{6}}{2}$

$V_{S.ABCD} = \frac{1}{3}.SO.S_{ABCD} = \frac{1}{3}.\frac{a\sqrt{6}}{2}.a^{2} = \frac{a^{3}\sqrt{6}}{6}$

Sau bài viết này, hy vọng các em sẽ nắm chắc được toàn bộ lý thuyết và bài tập áp dụng tính thể tích khối chóp tứ giác đều. Để có thêm nhiều kiến thức hay về công thức toán hình 12, các em có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ và chuẩn bị tốt cho kỳ thi đại học sắp tới nhé!

Tham khảo thêm:

Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết

>> Xem thêm:

12 công thức tính thể tích khối chóp kèm ví dụ cụ thể
Công thức tính thể tích khối tròn xoay và bài tập vận dụng
Công thức tính thể tích khối cầu nhanh và chính xác nhất
Công thức tính thể tích khối lăng trụ đứng đầy đủ nhất

Link nội dung: https://ausp.edu.vn/cong-thuc-tinh-the-tich-khoi-chop-tu-giac-deu-chi-tiet-va-bai-tap-a24002.html