Số chính phương là gì? Cách biết một số là số chính phương và ví dụ minh họa

Số chính phương là gì? Nó là một khái niệm quan trọng trong toán học mà học sinh trung học cơ sở cần hiểu rõ. Bài viết sau đây sẽ giải đáp mọi thắc mắc về số chính phương, từ định nghĩa đến tính chất. Liệu số 0 có phải là số chính phương hay không? Hãy cùng FPT Shop khám phá thông tin chi tiết này để nắm bắt kiến thức hữu ích!

Số chính phương là gì? Đặc tính của các số chính phương

Số chính phương là gì?

Số chính phương là một số nguyên dương mà có thể được viết bằng cách nhân một số nguyên với chính nó. Ví dụ, số 4 là số chính phương vì 4 = 2 x 2, và số 9 cũng là số chính phương vì 9 = 3 x 3. Trong các ví dụ này, chúng ta có thể thấy rằng số chính phương luôn là kết quả của phép nhân một số với chính nó.

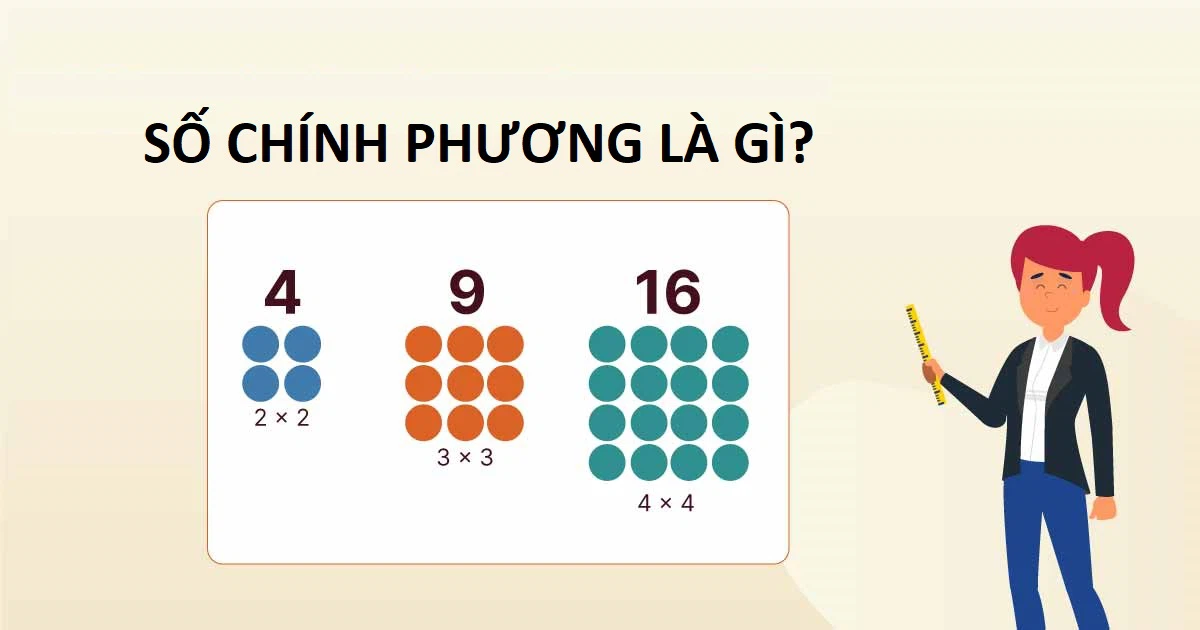
Tuy nhiên, không phải tất cả các số đều là số chính phương. Ví dụ, số 5 không phải là số chính phương vì không có số nguyên nào khi nhân với chính nó sẽ cho kết quả là 5. Tương tự, số 7 cũng không phải là số chính phương.

Các số chính phương đầu tiên là: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,...

Đặc tính của các số chính phương

Sau khi tìm hiểu định nghĩa về số chính phương là gì rồi, vậy ta cùng tìm hiểu các đặc tính chính của các số chính phương nhé!

Các đặc tính cơ bản của số chính phương là gì?

• Công thức: Một số chính phương có thể được biểu diễn dưới dạng n^2, trong đó n là một số nguyên. Ví dụ, 4 là số chính phương vì 4 = 2^2, và 9 là số chính phương vì 9 = 3^2.
• Tổng của các số lẻ liên tiếp: Mỗi số chính phương có thể được tính bằng cách cộng các số lẻ liên tiếp bắt đầu từ 1. Ví dụ, 4 = 1 + 3, 9 = 1 + 3 + 5, và 16 = 1 + 3 + 5 + 7.
• Chữ số cuối cùng: Trong hệ thập phân, chữ số cuối cùng của một số chính phương chỉ có thể là 0, 1, 4, 5, 6 hoặc 9. Ví dụ, 16, 25 và 36 đều là các số chính phương vì chữ số cuối cùng của chúng là 6, 5 và 6 tương ứng.
• Tính chất chia hết: Nếu một số chính phương chia hết cho một số nguyên tố, thì nó cũng chia hết cho bình phương của số nguyên tố đó. Ví dụ, nếu một số chính phương chia hết cho 3, thì nó cũng chia hết cho 9 (3^2).
• Cấu trúc hình học: Khi sắp xếp các số chính phương vào một dạng hình học, chúng có thể được sắp xếp thành các hình vuông. Mỗi điểm trên hình vuông biểu thị một số chính phương. Độ dài cạnh của hình vuông tương ứng với căn bậc hai của số chính phương.

Hy vọng rằng diễn giải này giúp bạn hiểu rõ và trả lời được thắc mắc “Các đặc tính của số chính phương là gì?”.

Số chính phương nhỏ nhất

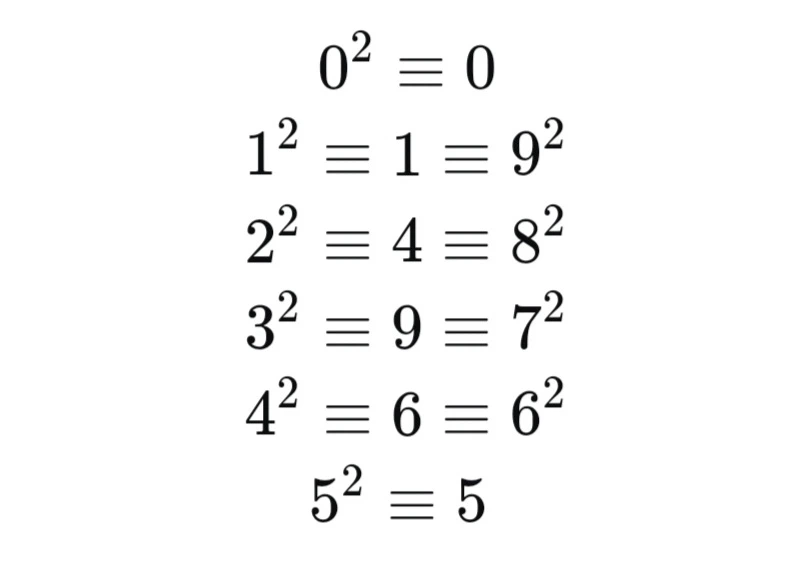
Số chính phương nhỏ nhất là số chính phương có giá trị nhỏ nhất.

Nếu chỉ xét các số tự nhiên dương, thì số chính phương nhỏ nhất là 1. Bởi vì 1 có thể biểu diễn dưới dạng bình phương của 1, tức là 1^2 = 1.

Tuy nhiên, nếu xét tất cả các số tự nhiên, bao gồm cả số 0, thì số chính phương nhỏ nhất là 0. Bởi vì 0 có thể biểu diễn dưới dạng bình phương của 0, tức là 0^2 = 0.

Ví dụ:

• 1 là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của 1, tức là 1^2 = 1.
• 4 là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của 2, tức là 2^2 = 4.
• 9 là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của 3, tức là 3^2 = 9.
• 16 là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của 4, tức là 4^2 = 16.
• 0 là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của 0, tức là 0^2 = 0.

Như vậy, tùy theo cách xét mà số chính phương nhỏ nhất có thể là 1 hoặc 0.

Số chính phương lớn nhất trong phạm vi số nguyên tố

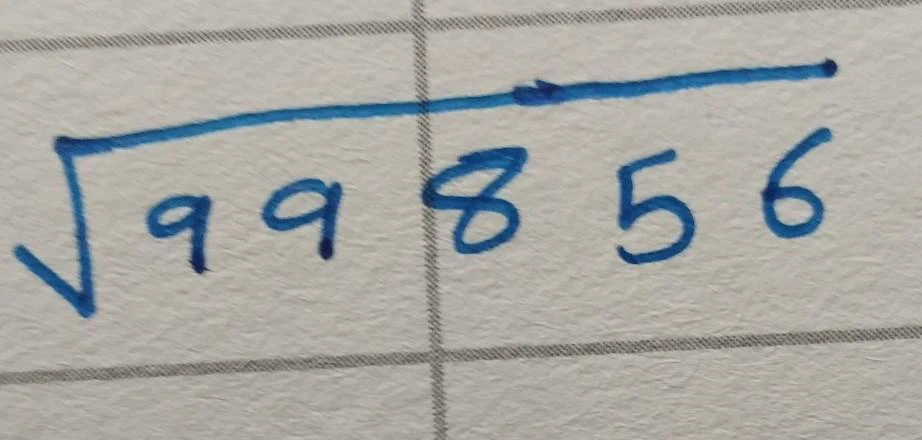
Số chính phương là số nguyên dương có thể được biểu diễn dưới dạng bình phương của một số nguyên dương khác. Ví dụ: 4, 9, 16, 25, 36, 49, 64, 81, 100 đều là số chính phương.

Trong mỗi phạm vi số nguyên tố, số chính phương lớn nhất có thể được xác định bằng cách tính bình phương của số nguyên tố lớn nhất trong phạm vi đó.

Ví dụ:

• Trong phạm vi số nguyên tố có 1 chữ số (từ 1 đến 9), số nguyên tố lớn nhất là 3. Do đó, số chính phương lớn nhất trong phạm vi này là 9 (bình phương của 3).
• Trong phạm vi số nguyên tố có 2 chữ số (từ 10 đến 99), số nguyên tố lớn nhất là 9. Do đó, số chính phương lớn nhất trong phạm vi này là 81 (bình phương của 9).
• Trong phạm vi số nguyên tố có 3 chữ số (từ 100 đến 999), số nguyên tố lớn nhất là 31. Do đó, số chính phương lớn nhất trong phạm vi này là 961 (bình phương của 31).
• Trong phạm vi số nguyên tố có 4 chữ số (từ 1000 đến 9999), số nguyên tố lớn nhất là 99. Do đó, số chính phương lớn nhất trong phạm vi này là 9801 (bình phương của 99).
• Trong phạm vi số nguyên tố có 5 chữ số (từ 10000 đến 99999), số nguyên tố lớn nhất là 316. Do đó, số chính phương lớn nhất trong phạm vi này là 99856 (bình phương của 316).

Như vậy, số chính phương lớn nhất trong phạm vi số nguyên tố có n chữ số là bình phương của số nguyên tố lớn nhất có n chữ số.

Cách nhận biết một số là số chính phương

Phần này chúng ta cùng tìm hiểu cách để nhận biết một số chính phương là gì nhé!

Để nhận biết số chính phương, bạn có thể dựa vào các cách sau:

Kiểm tra căn bậc 2

Căn bậc 2 của một số chính phương là một số tự nhiên. Do đó, nếu căn bậc 2 của một số là một số tự nhiên thì số đó là số chính phương.

Ví dụ:

9 là số chính phương vì căn bậc 2 của 9 là 3, và 3 là một số tự nhiên.

10 không phải là số chính phương vì căn bậc 2 của 10 là 3.16227766, và 3.16227766 không phải là một số tự nhiên.

Nhìn vào chữ số cuối cùng

Trong hệ thập phân, chữ số cuối cùng của số chính phương chỉ có thể là 0, 1, 4, 5, 6, hoặc 9. Nếu số không kết thúc bằng một trong các chữ số sau đây, thì nó không thể là một số chính phương.

Ví dụ:

16 là số chính phương vì chữ số cuối cùng của nó là 6.

23 không phải là số chính phương vì chữ số cuối cùng của nó là 3.

Phân tích thừa số nguyên tố

Một số chính phương có thể được phân tích thành thừa số nguyên tố với tất cả các thừa số nguyên tố có số mũ chẵn.

Ví dụ:

256 = 2^8 là số chính phương. Vì 256 có thể biểu diễn dưới dạng bình phương của 16 (16^2 = 256), và phân tích thành thừa số nguyên tố là 2^8.

Sử dụng bảng số chính phương

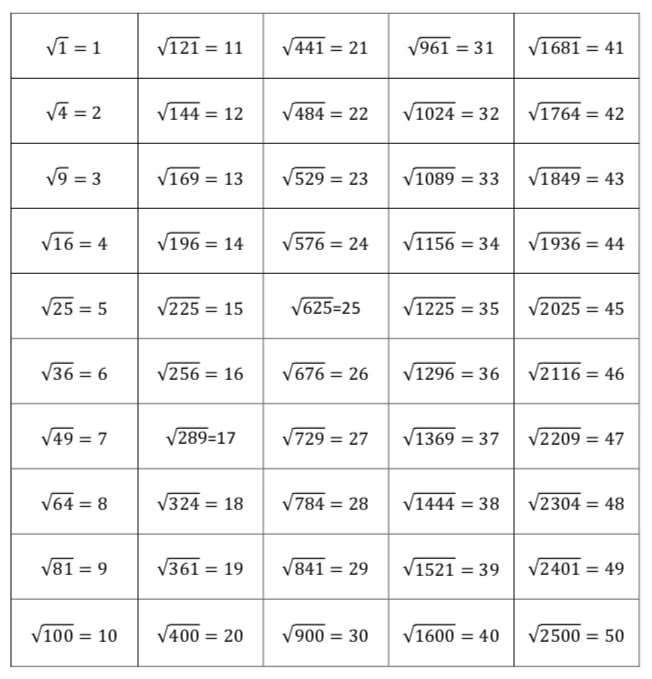
Nếu bạn cần kiểm tra số chính phương thường xuyên, bạn có thể sử dụng bảng số chính phương cơ bản. Ví dụ bảng số từ 1^2 đến 12^2 để tham khảo nhanh.

Sử dụng các công cụ tính toán

Khi đối mặt với các số lớn, việc sử dụng máy tính hoặc ứng dụng tính toán sẽ giúp bạn nhanh chóng xác định xem một số có phải là số chính phương hay không.

Trên đây là một số cách để nhận biết số chính phương. Bạn có thể chọn phương pháp phù hợp với nhu cầu của bạn.

Một số dạng bài tập về số chính phương

Vậy là bạn đã hiểu khái niệm số chính phương là gì, đặc tính của chúng và cách nhận biết một số có phải là số chính phương hay không, như 0, 1, 4, 9,… Hãy cùng thử sức với một số bài tập về số chính phương để hiểu rõ hơn về loại số này trong toán học.

Để luyện tập và hiểu rõ hơn về số chính phương, chúng ta hãy cùng luyện tập qua một số dạng bài tập đặc trưng sau đây:

Dạng 1: Chứng minh số chính phương

Ví dụ: Chứng minh rằng số B = 4n^4 + 4n^3 + n^2 là số chính phương với mọi số nguyên dương n.

Lời giải:

B = 4n^4 + 4n^3 + n^2 = n^2 x (4n^2 + 4n + 1) = n^2 x (2n + 1)^2

Ta thấy, B có thể được biểu diễn dưới dạng tích của hai bình phương. Hoặc B = [n(2n+1)]^2, và n(2n + 1) là một số nguyên. Vậy nên kết luận B là một số chính phương.

Dạng 2: Tìm n sao cho một số là chính phương

Ví dụ: Tìm số tự nhiên n sao cho số sau là số chính phương: B = n^2 + 4n + 1.

Lời giải:

Vì số B là chính phương, ta đặt n^2 + 4n + 1 = b^2

=> 4n^2 + 16n + 4 = 4b^2

=> (4n^2 + 16n + 16) -16 + 4 = 4b^2

=> (2n + 4)^2 - 4b^2 = 12

=> (2n + 4 + 2b) x (2n + 4 - 2b) = 12

Ta nhận thấy 2n + 4 + 2b > 2n + 4 - 2b, và đây đều những số nguyên dương. Vậy nên ta có thể tìm các cặp số tương ứng: (12,1), (6,2) và (4,3). Bạn cần xét đến từng trường hợp để tìm ra n và b. Cụ thể:

Trường hợp 1: (2n + 4 + 2b) x (2n + 4 - 2b) = 12 = 12 x 1 => n = 5/4, b = 11/4

Trường hợp 2: (2n + 4 + 2b) x (2n + 4 - 2b) = 12 = 6 x 2 => n = 0, b = 1

Trường hợp 3: (2n + 4 + 2b) x (2n + 4 - 2b) = 12 = 4 x 3 => n = -1/4, b = 1/4

Nhưng n là số tự nhiên, nên chỉ có đáp án n = 0, b = 1 là thỏa mãn. Và n = 0, suy ra số chính phương B = 1.

Tạm kết

Như vậy là bạn đã hiểu rõ hơn về số chính phương và cũng đã làm quen với một số dạng bài tập liên quan đến chủ đề này. Hy vọng rằng bạn đã có cái nhìn tổng quan về số chính phương là gì, đặc tính của chúng, cùng với việc giải đáp thắc mắc 0 có phải là số chính phương hay không. Chúc bạn học được nhiều kiến thức hữu ích từ bài viết này!

Xem thêm

Tawk to là gì? Những lý do bạn nên nhanh chóng cài đặt Tawk.to cho Website thương mại

Năm 2024 tuổi Dậu hợp màu gì? Tìm hiểu những màu sắc mang lại may mắn cho người tuổi Dậu

Git stash là gì? Hướng dẫn cách sử dụng lệnh Git stash effect hiệu quả cho người học lập trình

Bàn phím là thiết bị không thể thiếu đối với bất kỳ ai sử dụng máy tính. Một chiếc bàn phím tốt sẽ mang lại trải nghiệm gõ phím thoải mái, chính xác và hạn chế mỏi tay. Hiểu được nhu cầu của khách hàng, FPT Shop mang đến cho bạn đa dạng các mẫu bàn phím chính hãng từ các thương hiệu nổi tiếng với giá cả vô cùng hấp dẫn. Hãy đến FPT Shop để sở hữu cho mình một chiếc bàn phím chính hãng, giá tốt ngay hôm nay!

Bàn phím