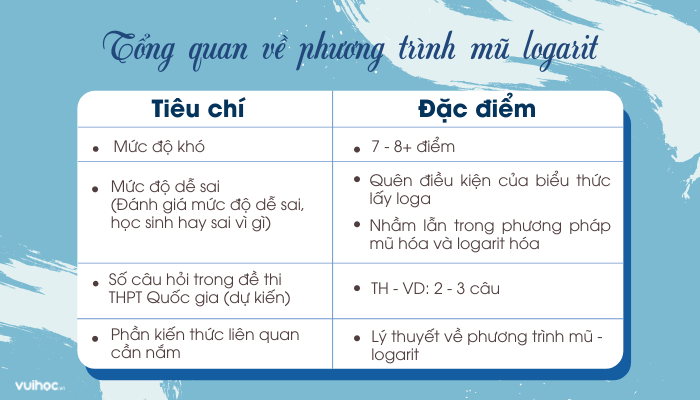
Trước hết, các em hãy đọc bảng dưới đây để có cái nhìn tổng quan nhất về các bài toán sử dụng cách bấm máy tính phương trình mũ logarit nhé!
Để dễ dàng hơn trong ôn tập, VUIHOC gửi tặng các em bộ tài liệu tổng hợp toàn bộ lý thuyết phương trình mũ logarit và các cách bấm máy tính phương trình mũ logarit. Các em nhớ tải theo link dưới đây nhé!
Tải xuống file tổng hợp lý thuyết cách bấm máy tính phương trình mũ logarit
Đặc biệt hơn, cuối bài sẽ có video bài giảng của thầy Thành Đức Trung hướng dẫn các mẹo bấm máy CASIO giải phương trình mũ logarit. Các em nhớ đọc đến cuối bài giảng nhé!
1. Ôn tập tổng quát về lý thuyết phương trình mũ logarit
1.1. Lý thuyết phương trình mũ
Về định nghĩa:
Hiểu đơn giản, phương trình mũ là dạng phương trình 2 vế trong đó có chứa biểu thức mũ.
Theo định nghĩa đã được học trong chương trình THPT, ta có định nghĩa và dạng tổng quát chung của toán 12 phương trình mũ như sau:
Phương trình mũ có dạng $a^x=b$ với $a,b$ cho trước và $0
Phương trình mũ có nghiệm khi:
Với $b>0: a^x=b\Rightarrow x=log_ab$
Với $b\leq 0$: phương trình mũ vô nghiệm
Các công thức phương trình mũ cơ bản cần nhớ:
Để thành thạo cách bấm máy tính phương trình mũ logarit, các em cần ghi nhớ các công thức cơ bản của số mũ phục vụ áp dụng trong các bước biến đổi. Công thức mũ cơ bản được tổng hợp trong bảng sau:
Ngoài ra, các tính chất của số mũ cũng là một phần kiến thức cần nhớ để thực hiện các cách bấm máy tính phương trình mũ logarit. Tổng hợp tính chất của số mũ được VUIHOC liệt kê theo bảng dưới đây:
Các em cần lưu ý, các tính chất trên áp dụng khi số mũ đó đã xác định nhé!
1.2. Lý thuyết về phương trình logarit - áp dụng cách giải phương trình logarit bằng máy tính
Về định nghĩa:
Với cơ số a dương và khác 1 thì phương trình có dạng như sau được gọi là phương trình logarit cơ bản $log_ax=b$
Ta thấy vế trái của phương trình là hàm đơn điệu có miền giá trị là R. Vế phải phương trình là một hàm hằng. Vì vậy phương trình logarit cơ bản luôn có nghiệm duy nhất. Theo định nghĩa của logarit ta dễ dàng suy ra nghiệm đó là $x=a^b$
Với điều kiện 0
Đối với phương trình logarit, chúng ta cần lưu ý thêm các công thức dưới đây để hiểu được phương pháp tự luận của cách bấm máy tính phương trình mũ và logarit:
Tham khảo ngay bộ tài liệu ôn tập kiến thức và phương pháp giải mọi dạng bài tập trong đề thi Toán tốt nghiệp THPT

2. Chi tiết cách bấm máy tính phương trình mũ và logarit
2.1. Sử dụng chức năng CALC trong cách giải phương trình logarit bằng máy tính
Ở dạng sử dụng chức năng CALC để thử đáp án này, ưu điểm của cách bấm máy tính phương trình mũ logarit này là thực hiện nhanh, dễ hiểu, dễ làm. Tuy nhiên, phương pháp này có nhược điểm là chỉ giải được những dạng phương trình cho sẵn nghiệm ở dưới đáp án.
Phương pháp giải chi tiết:
- Bước 1: Nhập phương trình vào máy tính
- Bước 2: Dùng CALC các giá trị x ở đáp án xem đáp án nào cho kết quả bằng 0 thì chọn.
Ta cùng xét ví dụ minh hoạ cách bấm máy tính phương trình mũ logarit dưới đây:
Ví dụ: Phương trình $log_2x.log_4x.log_6x=log_2x.log_4x+log_4x.log_6x+log_6x.log_2x$ có tập nghiệm là:
A. {1}
B. {2,4,6}
C. {1,12}
D. {1,48}
Giải
Phương trình mới có dạng: $log_2x.log_4x.log_6x-(log_2x.log_4x+log_4x.log_6x+log_6x.log_2x)=0$. Nhập vào máy tính vế trái của phương trình.
Tại X=1, ta bấm “CALC + 1 + =” > Phương trình = 0.
Vậy X=1 là nghiệm của phương trình, chúng ta loại được đáp án B.
Tại X=12, ta bấm “CALC + 12 + =” > Phương trình ra đáp án khác 0.
Vậy X=12 không là nghiệm của phương trình. Loại đáp án C.
Tại X=48, ta bấm “CALC + 12 + =” > Phương trình = 0.
Vậy X=48 là nghiệm của phương trình.
Suy ra, đáp án D là đáp án đúng.
Lưu ý, đối với phương trình mũ ta làm tương tự như ví dụ.
2.2. Cách giải phương trình logarit bằng máy tính sử dụng chức năng SOLVE để tìm nghiệm
Ưu điểm của cách bấm máy tính phương trình mũ logarit này là bài nào cũng có thể giải được. Nhưng ngược lại, có một số bài toán phức tạp thì máy tính cần mất rất nhiều thời gian để chờ ra kết quả.
Cách giải phương trình logarit bằng máy tính chi tiết:
- Bước 1: Chuyển vế đưa về dạng $f(x)=0$
- Bước 2: Nhập $f(x)$ vào máy tính
- Bước 3: Ấn SHIFT rồi ấn SOLVE nhập giá trị x bất kỳ, ấn bằng và chờ kết quả.
Ta cùng xét ví dụ cách bấm máy tính phương trình mũ logarit như sau:
Ví dụ: Cho các số thực dương a, b thỏa mãn $log_9x=log_{16}(a+12log_9x)$. Tính x.
Giải
Nhập phương trình $log_9x-log_{16}(a+12log_9x)=0$ vào máy tính như hình dưới.
Bấm SHIFT + CALC.
Lưu ý: Khi máy tính hiện Solve for X? bạn có thể nhập giá trị X bất kỳ.
Tại đây máy sẽ cho ra một kết quả khá lẻ là 39.4622117. Tới bước này, đối với bài toán trắc nghiệm, bạn có thể so với từng đáp án đã cho để tìm ra đáp án đúng nhé.
2.3. Sử dụng chức năng TABLE trong cách giải phương trình logarit bằng máy tính
Đối với cách bấm máy tính phương trình mũ logarit này, ưu điểm là thực hiện nhanh hơn cách sử dụng SOLVE và làm được nhiều dạng bài. Nhưng nhược điểm của nó là chỉ giải được những bài có nghiệm bé.
Các bước giải chi tiết:
- Bước 1: Ấn mode 7 (fx-580 thì ấn menu 8)
- Bước 2: Nhập phương trình vào máy tính (nếu phương trình chưa bằng 0 thì phải chuyển vế trước khi nhập)
- Bước 3: Nhập các giá trị Start, End và Step
- Bước 4: Kiểm tra kết quả $f(x)$:
Nếu $f(x)$ đổi dấu từ âm sang dương hoặc ngược lại thì sẽ có 1 nghiệm nằm trong khoảng đó
Nếu $f(x)=0$ hoặc xấp xỉ bằng 0 thì có 1 nghiệm tại vị trí đó
Ví dụ minh hoạ sau đây sẽ giúp các em hiểu hơn về cách bấm máy tính phương trình mũ logarit này:
Ví dụ: Tính tích các nghiệm của phương trình sau: $log_3(3x).log_3(9x)=4$.
- Bước 1: Bấm MODE > 7 > Nhập hàm số: $f(x)=log_3(3x).log)3(9x)-4$.
- Bước 2: Nhấn “=” > Chọn START = 0 > “=” > Chọn END = 29 > “=” > Chọn STEP = 1 > “=”.
- Bước 3: Dò cột $f(x)$ để tìm những khoảng hàm số đổi dấu. Ví dụ như hình dưới đây ta thấy khoảng $(0;1)$ và $(1;2)$ hàm số đổi dấu từ âm sang dương. Vậy trên khoảng này sẽ có khả năng có nghiệm, ta sẽ xét tiếp 2 khoảng này.
Dò khoảng nghiệm của phương trình
- Bước 4: Bấm AC và dấu = để làm lại các bước trên. Với khoảng (0;1) ta chọn START = 0 > END = 1 > STEP 1/29. Ta được khoảng (0;0,0344) có thể có nghiệm, ta sẽ dò tiếp khoảng này để tìm nghiệm gần đúng nhất.
Dò tiếp khoảng nghiệm nhỏ hơn
- Bước 5: Với khoảng (0;0,0344) ta chọn START = 0 > END = 1 > STEP = 0,0344/29. Ta được nghiệm nằm trong khoảng (0,0189-0,0201).
Ra khoảng nghiệm gần đúng thứ 2
- Bước 6: Muốn có nghiệm chính xác hơn nữa ta lặp lại với START = 0,0189 > END = 0,0201 > STEP = (0,0201-0,0189)/29. Ta được nghiệm đúng thứ nhất là 0,01997586207.
Tìm ra nghiệm thứ nhất của bài toán
- Bước 7: Làm tương tự với khoảng (1;2). Ta được nghiệm đúng thứ hai là 1,852482759.
Tìm ra nghiệm thứ hai của bài toán
- Bước 8: Bấm tích hai nghiệm với nhau ta thu được kết quả của bài toán.
3. Bài tập vận dụng
Để thành thạo cách bấm máy tính giải phương trình mũ logarit thật nhanh, các thầy cô VUIHOC đã tổng hợp và biên soạn file bài tập vận dụng cách bấm máy tính phương trình mũ logarit có giải chi tiết. Các em nhớ tải về để luyện tập hằng ngày nhé!
Ngoài ra, thầy Thành Đức Trung cũng dành tặng các em video bài giảng về cách giải CASIO phương trình mũ logarit với vô cùng nhiều các mẹo làm bài cực hay. Các em đừng bỏ qua nhé!
Trên đây là toàn bộ lý thuyết tổng hợp về phương trình mũ và logarit cùng các cách bấm máy tính phương trình mũ logarit thông dụng nhất. Chúc các em có sự chuẩn bị tốt nhất trong quá trình ôn thi Toán THPT Quốc Gia sắp tới.